Repérage dans le plan
I] Repère et Coordonnées
1) Repere
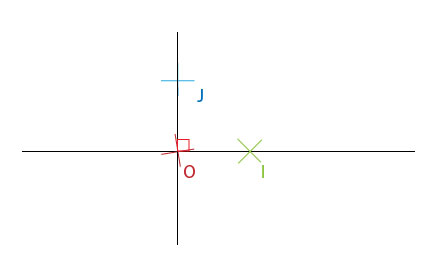
-Un repère de plan est défini par 3 points ( par exemple O, I, J ), qui ne sont pas alignés.
- La droite (OI) est l'axe des abscisses (x) et la distance qu'il y a entre {O} et {I} est l'unité de cet axe. En gros si la distance entre OI = 1 carreau, l'unité de l'axe des x sera de 1 carreau (l'unité c'est la distance entre deux nombres entiers qui se suivent ( comme 0 et 1 ), lorsque l'on met le point A à x=0, le point B se trouvera là où x=1 soit 1 carreau plus loin).
- Sur le même principe, la droite des ordonnées (y) est définie par OJ
- O est l'origine du plan, soit le point où les axes X et Y se croisent.
Ce qui donne :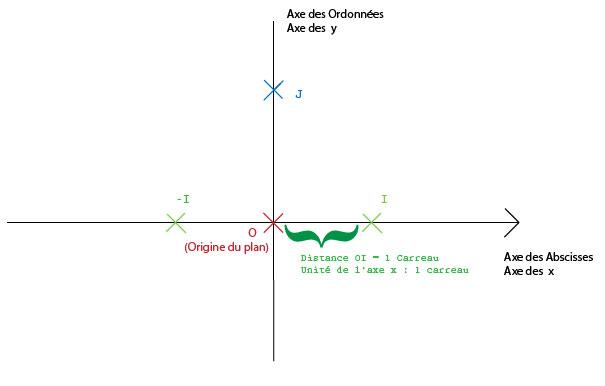
Ainsi, si on a un repère O, I, J,
Si les droites OI et OJ sont perpendiculaires, on dit du repère qu'il est Orthogonal.
Si en plus d'être perpendiculaires, la distance OI = OJ, le repère est defini comme Orthonormé
Exemple :
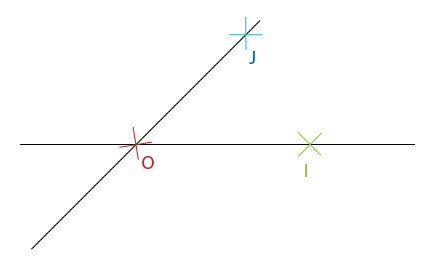
Repère Quelconque :
- Sans caractéristique.
Repère Orthogonal :
- Axes perpendiculaires
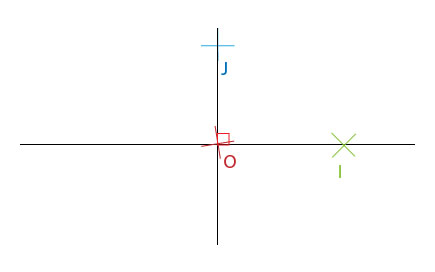
Repère Orthonormé :
- Axes perpendiculaires
- OI = OJ
3 )Coordonnées du milieu d'un segment ( J'ai passé le "2)" parce que je trouve qu'il embrouille. Ce qu'il y a en retenir, c'est qu'un point M dans un repère est défini par ses uniques coordonnées qui se notent M(X;Y).)
Propriété :
Soit le repère (O, I, J)
Soient A(xA;yA) et B(xB;yB) :
Le milieu de [AB] (qu'on appellera K) à pour coordonnées :